A few posts ago I added super-sampling to the ray tracer to help take care of jaggies. If you remember, this consisted of sending more rays into the scene. There is a cost of sending in all of these added rays. Thinking back on the picture of the circle and the super-imposed grid we really only needed to fix the edges, the center of the circle didn't change at all. So we really wouldn't need to do anything to fix the non-existant jaggies in the center of the circle. So, in order to save on processing by not tracing any more rays than we absolutely have to while still looking good. In order to do this I wrote an adaptive super-sampling algorithem, well actually two of them. They both work off of the same idea that we've traced enough rays when tracing one more ray affects the average of all previously traced ray by only a very small amount.
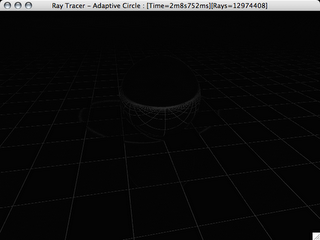
The first technique I wrote used a circular sampling area. The first step was to cast 8 rays around the perimeter of a circle centered at the current pixel. If the color of the center pixel was more than some epsilon from the average of the pixels on the radius we start casting more rays. We cast a random ray from withen the area of the circle and we keep casting until the difference between the current average and the average containing on more ray is less than epsilon. The left image is the normal render, the right one shows the number of rays cast for each pixel, the whiter the pixel the more rays cast. This graphically shows the adaptive aspect of the algorithem. You can see how along the edges more rays are cast than in the middle of square all the same color.
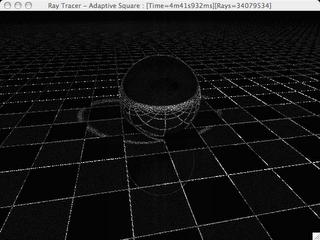
The second technique uses squares instead of circles, it starts by casting a ray for each point on a 2x2 grid and compares that average to the color at the center pixel, if the diffreence between them is greater than epsilon we increase the width of the square to 3, making it a 3x3 grid, compare that average to the grid before, if the difference is greator than epsilon keep repeating till is falls below epsilon.
If we increase epsilon to 1x10
-7, for the previous images it was at 1x10
-5, we can see a drastic improvment in the shadow edges.
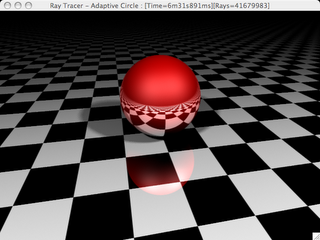
An interesting thing to note, if you click on the image it shows you the full size image and on the title bar are some statistics about the render, including time and number of rays cast. Notice that for this image of the the sphere about 41.7 million rays were needed on an 640x480 (307,200 pixels) image. That is about 136 rays per pixel. To get this same rays per pixel ratio without an adpative algorithem would use about a 12x12 square grid. Here is an image using a non-adaptive supersampling algorithem with a 12x12 grid, compare this to the previous image.